The Corequisite Reform Movement: A Higher Education Bait and Switch
Alexandros M. Goudas (Working Paper No. 5) March 2017 (Updated May 2020)
Let me begin by stating unequivocally that I, along with many others in the field of postsecondary education, support the thoughtful and holistic implementation of the original Community College of Baltimore County (CCBC) Accelerated Learning Program model (ALP) as studied by the Community College Research Center (CCRC) in 2010 (Jenkins et al., 2010) and 2012 (Cho et al., 2012). It is a comprehensive framework which can modestly improve outcomes in college-level English for remedial students just beneath the highest placement cutoff. Even if I and others support that exact ALP model, there are many important and little-known factors one needs to consider before supporting the corequisite reform movement as a whole, a movement which has gained an astonishingly rapid level of acceptance and implementation across the nation.
The most important factor to consider is that because some institutions are trying to cut costs, and others have wanted to limit remediation because they view it as ineffective or a barrier (Fain, 2012), a good idea for increasing college-level course outcomes has switched into a convenient and seemingly data-based model to allow institutions to fast-track and bypass remediation, all without the level of support in college-level courses that was initially recommended and studied. In other words, using ALP as a basis, some institutions are implementing versions of corequisites that are nothing more than placing remedial students into college-level courses and adding one lab hour as the sole means of support. These variations are not based on research, and therefore they resemble a bait-and-switch scheme. In order for the reform to qualify as a true bait and switch, of course, it must be intentional. Indeed, it is clear that some organizations, such as Complete College America (CCA), are engaging in the promotion of low-support corequisites solely as a means by which to limit or eliminate remediation. However, others are engaging in similar switches unintentionally. Regardless of intent, nevertheless, the corequisite reform movement may be harming at-risk students more than helping them.
For example, the rapidity of the model’s acceptance into higher education has led some institutions, even CCBC itself, to claim it is so effective that they think it is appropriate to cut access to all stand-alone remedial courses for students in that level (ALP, n.d.-a). This is concerning because some slight tricks in the data analyses of corequisites, another form of bait and switch, are making the relatively moderate, short-term results of the program appear much better than they actually are. If this reform movement gets even more traction, it may end up inadvertently or intentionally, depending on the institution, causing the loss of appropriate access and support for millions of at-risk college students.
With so much on the line, policymakers would do well to fully understand the corequisite model, its variations, the few studies on ALP, and what the data really show. Since there are a great deal of key factors surrounding corequisites that many people have not yet considered, this article is designed to cover the model quite thoroughly. It is also divided into many sections that build on one another because understanding the entire corequisite reform movement can be surprisingly complicated. Once all of these factors are understood and considered as a whole, educators and lawmakers can make more thoughtful, data-based decisions about whether or how to proceed with the implementation of a corequisite model.
the Original Corequisite model: What is alp exactly?
In the original ALP model, as studied by the CCRC in 2010 and 2012 (Cho et al., 2012; Jenkins et al., 2010), eight remedial students in English writing who scored just beneath the college-level placement cutoff volunteered to be placed not into a stand-alone remedial writing course, but instead into two courses, one of which was a three-credit college-level English composition course that had twelve nonremedial students in it. The other course was termed the “companion course,” a class which was not actually remedial English. Rather, it was a three-credit course designed to get the eight remedial English students from the combined college composition course to be able to understand and complete the college-level English material successfully. In other words, eight remedial students took a college-level English composition course with twelve nonremedial students for three hours a week, and then those same eight students took another three-hour companion course, this time without the nonremedial students, and both courses had the same instructor.
The companion course’s curriculum has been characterized by Peter Adams, the founder of ALP, as the “deep version” of college composition (Adams et al., 2009). The instructor of the companion course did whatever it took to get the eight remedial students to master the college-level course’s objectives. On the ALP website, one can find seven bullet points outlining what the ALP instructors are aiming to accomplish in the companion course. Here are a few: “answering questions left over from the 101 class; discussing ideas for the next essay in 101; reviewing drafts of essays the students are working on for 101” (ALP, n.d.-b, para. 8). Most of the objectives were designed to allow students to spend more time on the material from the college composition course. As Adams et al. (2009) put it, “It’s more like a workshop for the ENGL 101 class” (p. 58). There was also a strong focus on student success strategies in the companion course.
It is important to understand the essential components and framework of this original model. First, what Adams et al. (2009) did was to lower the college-level composition placement cutoff by a little, allow only eight remedial students who were near the placement cutoff to volunteer to take a college composition course, and then make up for it by nearly doubling the time on task for these eight students in that college-level course (Jenkins et al., 2010). Indeed, this decision has data supporting it: There is some research showing that increasing the time that students engage in deliberate practice on a skill or topic will improve outcomes regardless of the course or level (Chickering & Gamson, 1987; Goodlad, 1984; Shafer, 2011).
Second, the model reduced the student-teacher ratio in the companion course (Jenkins et al., 2010). The college-level course had a student-teacher ratio of 20-1 (12 college-level students and 8 remedial students), and the companion course with the remedial students alone only had an 8-1 ratio. The stand-alone remedial courses in the traditional model of English remediation at CCBC had a 20-1 student-teacher ratio, so the ALP companion course more than halved the student-teacher ratio.
Third, both courses were taught by the same highly trained and motivated instructor who used normed materials (Adams et al., 2009). Two-thirds of the ALP instructors were full-time faculty members and one-third were adjuncts (Jenkins et al., 2010), but all ALP instructors went through extensive training and used a well-planned, unified curriculum sourcebook for the companion course that the ALP developers refined over time. The instructors chose to be a part of the program initially, and they received support from ALP coordinators and leaders. It is well understood that people who support a program will often work harder at that program, so these instructors were most likely highly motivated as well. Furthermore, the textbooks, the curriculum, the pedagogy—all were normed and discussed before implementing the program. All of this helps tremendously when it comes to learning outcomes.
Each of these key components—asking motivated students to participate voluntarily; doubling the time on task in English composition; reducing the student-teacher ratio by half or more in a course; utilizing highly motivated instructors who believe in the program; giving the instructors extensive professional support and training; unifying the curriculum; focusing on student success strategies and noncognitive issues—should individually be able to improve student outcomes in any course, let alone when combined. When ALP lowers the college-level cutoff slightly to allow upper-level volunteer remedial students to receive a combination of all of these interventions, there is good reason to believe that those remedial students will perform better in college-level English composition. They are thoughtful interventions; they are innovative when put all together in a well-supported framework. It appears to be an effective way to invest in remedial students and to increase their ability to understand and practice college-level English composition outcomes. So what research is out there on this ALP model, and what does the data say about the results?
what research on the alp model exists?
The CCRC studied the exact CCBC ALP model described above in two different articles, the first one in 2010 and the second as a follow-up in 2012 (Cho et al., 2012; Jenkins et al., 2010). No one would disagree with the fact that the CCRC has had the most qualified statistical researchers dedicating the most time, money, and effort to studying community college subjects like corequisites. The CCRC is the single-most cited research institution undergirding the corequisite reform movement. Almost every document or article on corequisites has footnotes, end notes, quotes, or citations referring to the CCRC’s work as the foundation for implementing the model.
Contrary to claims of its efficacy (Vandal, 2015), however, the corequisite model has not been studied thoroughly enough to justify its level of implementation in the nation. In fact, even the CCRC in their latest paper on a state-wide corequisite initiative in Tennessee, a model which is a variation of the ALP original, admitted that the “corequisite model has not yet been subjected to rigorous evaluation” (Belfield et al., 2016, p. 8). Therefore, Davis Jenkins, a top CCRC researcher who coauthored three seminal papers on corequisites, characterized his own body of research as not “rigorous evaluation,” yet this body of three papers is the most in-depth and well-constructed set of studies on the original ALP and one of its variations.
However, another reputable study that should be included in the body of data-based literature on corequisites (Logue et al., 2016). It is the only randomized controlled trial on corequisites to date, and it investigates a version of corequisite math. This study will be covered more in subsequent sections of this paper, but its intervention differs from the ALP corequisite model sufficiently enough that it should be classified as a separate intervention. The main reason for this classification is that remedial students in this intervention did not take two courses simultaneously, which was the original design (taking a remedial course not as a prerequisite but as a corequisite). They took a college-level course along with a structured lab. Of course, this model is one of the many variations of corequisites being touted in the nation, but thus far, there is only one randomized controlled trial involving this variation that can be considered worthy of citing.
There are, however, other organizations claiming miraculous results from various state corequisite models. Complete College America (CCA) appears to be the most vocal advocate of corequisites, and they have dedicated a great deal of money and time promoting the model. CCA claims to have data supporting the results from five different states: Georgia, West Virginia, Tennessee, Indiana, and Colorado. One can view some of these numbers on a website called “Spanning the Divide,” complete with animated infographics (Complete College America, n.d.).
At the foot of this site, however, the only link to any actual data underlying these claims is a four-page descriptive document entitled “methodology,” which simply provides an overview of self-reported information that representatives of the states involved with corequisites presented to CCA. The document does not actually contain data to support the percentages from the infographics. When one investigates some of the self-reported data in this document, such as the numbers from Georgia, one can only find more descriptive information and not any data on outcomes, much less any data analysis.
Additionally, as can be read on the second page of CCA’s methodology document, people are free to request more “detailed information on state data.” I did request this data, and the spreadsheet I received had raw numbers of remedial passrates and graduation rates from approximately thirty states. Other than repeating the same percentages from the website, the spreadsheet contained no underlying data supporting them. There appears to be no statistical analyses whatsoever. After repeated inquiries, I was never sent any additional data by CCA on corequisites in the nation. Interestingly, I was told that I would have to inform them about how I would be using any more of their data before they could share it with me. I replied that I would be authoring this article and speaking about corequisite research, and they never responded.
Therefore, it is safe to conclude that the current self-reported information from CCA is not quality research and analysis into the effects of corequisites. Thus far, then, only the CCRC (Belfield et al., 2016; Cho et al., 2012; Jenkins et al., 2010) and Logue et al. (2016) can claim that their papers contain accurate and reliable data analyses on any corequisite model’s outcomes, even if the CCRC has characterized their own research as not rigorous.
Finally, a more recent study on the Tennessee model of corequisites studied only the students just above and beneath the college-level cutoff (Ran & Lin, 2019). It is rigorous, and can be added to the corpus of literature on corequisites, but is also limited in scope because it did not assess outcomes for students below the cutoff, which comprised most of the students taking corequisites in Tennessee. There are other models of corequisites that have been studied in with more rigorous methods, but they are not in English or mathematics (Goudas, 2019). Therefore, these five (Belfield et al., 2016; Cho et al., 2012; Jenkins et al., 2010; Logue et al., 2016; Ran & Lin, 2019) are the most reliable in terms of data, methodology, and more generalizability.
What are the alp results according to ccrc research?
The CCRC studied the exact ALP program described above in two articles, one following up on the other (Cho et al., 2012; Jenkins et al., 2010). They tracked and compared two groups at CCBC: 1) the absolute number and percent of students who were below the college-level cutoff, who went through the traditional stand-alone upper-level remedial English writing course, and then who completed the respective college-level English course; and 2) the absolute number and percent of similarly qualified remedial students who chose to go through the ALP version, which means they took the companion course and the college-level English course simultaneously. The CCRC also then created some like-comparison groups using propensity score matching. That is, researchers created two groups from all ALP and non-ALP students that were as similar as possible with regard to demographic and cognitive characteristics; their matched groups had 592 students each (Cho et al., 2012, p. 6). The best analysis to consider is this matched group analysis because it addresses some of the problems with apples-to-oranges comparisons.
At first glance, there are several positive results which can be taken from the matched group analysis (Cho et al., 2012). The most positive is that many more students passed the college-level English composition course under the ALP model (28.5 to 31.3 percentage points more likely, which is about 75 to 80%). There was also a modest increase in passrates in the second college composition course (16.5 to 18.5 percentage points higher), as well as a slight increase in persistence rates into the second year for ALP students (10.5 percentage points). Moreover, ALP’s model showed a small increase in college courses attempted (1.1 courses more) and completed (.5 more), and college credits taken (2.5) and completed (1.6) as compared to non-ALP remedial students. As with most research, however, there are a great deal of caveats to these positive results. Some or most of these results might be due to selection bias, a relatively small dataset in the matched groups, and instructor effects.
Before addressing the positive results’ caveats, there were some negative results which need to be highlighted. First, and this was somewhat surprising, the nonremedial college-level students who took their college composition course with ALP students had lower subsequent college-level enrollment and passrates. That means when college-ready students were placed into a college English composition course with eight remedial students, those twelve college-level students performed worse in subsequent college-level courses than did other college-ready students who took college composition in a section with no remedial students. The negative results for nonremedial students mirrored that of the positive ALP results: There was a slight decrease in persistence rates into the second year for nonremedial students (3 percentage points); there was a small decrease in college courses attempted (.5 courses less) and completed (.5 less), and there was a decrease in college credits taken (1.4) and completed (1.5) (Cho et al., 2012).
Most importantly, nonremedial student transfer rates (one of three completion metrics studied) were statistically significantly lower due to participation in ALP (4 percentage points lower) (Cho et al., 2012). Since more nonremedial students participated in ALP than remedial students (12 compared to 8), the subsequent negative effects of ALP on nonremedial students outweigh the subsequent positive effects by a factor of nearly 50%. All this shows that the model negatively affected nonremedial students, perhaps because the instructor taught at a lower overall level in an ALP section, thus teaching to the middle. Cho et al. did not discuss possible reasons why these college-ready students were negatively affected by being in an ALP section, but they minimized the negative impact by stating that the increase in passrates by ALP students more than made up for it (p. 21).
More significantly, the graduation rate for ALP students did not change compared to traditional remedial students (Cho et al., 2012). In fact, ALP had a negative impact on all three completion metrics that the CCRC studied, but two were statistically insignificant decreases (associate attainment and transfer rate). Regarding the other completion metric, Cho et al.’s balanced matched cohort regression analysis showed that being a part of the model caused a statistically significant decrease in the ability for ALP students to earn a certificate (p. 20). This is perhaps the most discouraging result from the CCRC studies because the ALP model more than doubles the cost of remediation.
A crucial caveat to the moderately improved outcomes for ALP students is that in the original model studied, ALP students were volunteers (Jenkins et al., 2010). In other words, this was not a randomly assigned intervention; ALP participants were instead given the option to join. This is a classic example of selection bias, and it might have significantly affected outcomes. Jenkins et al. recognized this distinct possibility: “Given that the ALP program is voluntary, it is also possible that student selection bias could be responsible for the higher success rates of ALP students” (p. 3). Even though Jenkins et al. moderated this statement by claiming that students in both groups, ALP and non-ALP, have similar demographics, they could not account for noncognitive factors that spur motivated students to perform better in many cases (Duckworth & Yeager, 2015). This casts a shadow on all ALP’s positive results in the two articles.
Another limitation to the study has to do with instructor quality and the impact that had on ALP students. Researchers from the Jenkins et al. (2010) paper found that “when [they] added controls for instructor effects, [they] found that ALP students were less likely to be retained and to attempt college-level courses” (p. 11). Even though the 2012 paper’s findings reversed these findings, Cho et al. may have participated in inadvertent p-hacking to create the matched sample (Aschwanden & King, 2015). To explain, Cho et al. (2012) discarded approximately 90% of the non-ALP potential sample (4,953 of a total of 5,545) when creating the “balanced matched samples” (p. 6). It is quite possible that if different matched samples were formed from the other 4,953 remaining non-ALP students, the results would be different for each sample of 592. Even the best researchers and publishers in the world have problems with reproducibility, p-hacking, and publication bias (Aschwanden & King, 2015; Ioannidis, 2005; Nosek, 2015).
In the final analysis, the few positive outcomes of ALP are offset by several problems. First, the increase in passrates in college composition may have been affected by selection bias. These passrates may also have been increased solely due to the fact that ALP students received double the time on task and half the student-teacher ratio, both of which double the cost of remediation and which should have independent positive effects on students regardless of their use in the ALP model. Second, the increases in college-level credits attempted and completed—1.1 courses more taken and half a course more passed respectively—are not very large when they are explained in prose and not statistics. Third, the increase in total college credit accumulation (1.6 more credits for ALP students) is also relatively small, temporary, and may be explained by selection bias. Fourth, almost all increases in outcomes for ALP’s remedial students are matched with equal decreases in outcomes for nonremedial students. Finally, the most important outcome that overshadows any positive results, especially the increase in college composition passrates and persistence, is that graduation rates were no higher for ALP students. In fact, in the case of certificate attainment, completion rates were slightly negatively affected by participation in ALP (Cho et al., 2012).
There are several other negative consequences that need to be explored for the entire picture of the results of ALP to be understood. The first involves the costs of the program.
alp costs more than double the traditional model
The ALP model greatly increased instructional expenditures due to two factors. First, the traditional stand-alone remedial courses at CCBC had a student-teacher ratio of 20-1 and the ALP model is 8-1 (Cho et al., 2012; Jenkins et al., 2010), so the instructional costs for remedial students under the ALP model was greater by more than a factor of two. The current ALP model has shifted to a 10-1 student-teacher ratio (ALP, n.d.-b), so CCBC has since reduced costs somewhat, but even at 10-1, it still costs twice as much to teach the same number of remedial students. Second, whereas perhaps half of stand-alone remedial students ended up enrolling in a college-level composition course under the traditional model due to attrition, in the ALP model, all remedial students take both a remedial course and a college-level course simultaneously. This increases instructional costs by approximately another 30%.
Both of these factors more than double the cost of instruction for the ALP model when compared to the traditional model. The Belfield et al. (2016) paper acknowledged this when researchers found that “the costs of corequisite remediation are significantly higher than those of prerequisite remediation: many more students are enrolled in college-level courses who would not have been previously because they would not have completed their remedial sequences” (p. 7). Jenkins et al. (2010) stated that “the college found that ALP costs almost twice as much per year as the traditional model” (p. 3).
Careful analysis of their hypothetical cost calculations in the Jenkins et al. (2010) paper reveals, however, that they did not take into consideration the extra sections that were required to be added due to the 8-1 student-teacher ratio in the original ALP model. In other words, if 100 traditional remedial students had been taught at the CCBC before ALP, it would have required 5 sections of 20 students taught by 5 instructors. Once ALP was implemented, and, for example, 40 students participated in it, that would have resulted in 8 total sections to cover those same 100 students (5 sections of 8 ALP students, and 3 sections of 20 traditional remedial students). For 40% of the students to participate in the ALP, that is a 60% increase in the instructional costs for the same number of students.
Depending on how many sections of ALP are offered, that number would rise to a possible 220% of instructional costs. In other words, if 80 of 100 remedial students participated in ALP, then that would be 11 sections required, 10 ALP and 1 traditional, which is 6 more sections than the original 5 required for 100 traditional remedial students. Add to this scenario the fact that a third more students would be immediately enrolled in gateway and companion courses under the ALP model, and the result is well over double the cost when compared to the traditional model of remediation.
Instead of Analyzing graduation rates, the Analysis is “cost per successful student in Gateway Courses”: the first bait and switch in data analysis
Despite the fact that “ALP costs almost twice as much per year” (Jenkins et al., 2010, p. 3), researchers claimed that “the improvement in the college-level gateway pass rate more than compensates for these extra costs” (Belfield et al., 2016, p. 6). In all three papers, authors included or referred to a cost analysis that calculates the amount spent “per successful student” in college-level English (Belfield et al., 2016, p. 6; Cho et al., 2012, p. 1; Jenkins et al., 2010, abstract). They claimed that it is less expensive to use corequisites because more students pass gatekeeper English with the ALP model. In order to make this argument, researchers used two slight bait-and-switch data analyses which need to be examined thoroughly.
First, accepting this new definition of success is an abrupt shift away from higher education’s agreed-upon goal to increase completion (Russell, 2011). For many institutions of higher education, at some point in the last ten years the focus on the completion agenda imperceptibly switched to the short-term goal of completing of gatekeeper English and math. As CCA put it, “Where once there was a bridge to nowhere but college debt, disappointment and dropout, today there is a new, proven bridge to college success [referring to college-level courses]” (Complete College America, n.d.). Educators were baited into believing that completion of college was the ultimate goal for students involved in the reform, but this goal was somehow switched to the completion of a gatekeeper math and English course.
Belfield, Jenkins, and Lahr (2016) put the change of focus this way:
Many colleges and state systems are redesigning their remedial programs with the goal of ensuring that many more academically underprepared students take and pass college-level gateway courses and enter a program of study as quickly as possible. Low completion rates in remedial sequences and subsequent low retention into college-level courses suggest that remedial programs often serve as an obstacle to student progression. (p. 1)
In a more recent research brief, Jenkins and Bailey (2017) used correlational data to argue that students who pass gateway courses were much more likely to graduate, so therefore colleges should focus on getting students to pass these gateway courses instead of focusing on long-term metrics like graduation. The assumption underlying this new definition of success is that if more remedial students are able to get into and pass gateway courses, they stand a higher chance at graduating. Intuitively, this hypothesis appears to be correct.
However, this is essentially the remediation is a barrier argument, and unfortunately there is little evidence supporting this theory. If it were true that remediation is a barrier, then remedial students in the City University of New York’s remedial Accelerated Study in Associate Programs (ASAP) model (Scrivener et al., 2015), with stand-alone remedial courses being taken first, would not have had the astounding graduation rates they attained. Additionally, research has shown that first-year college-level courses are holding students back just as much as English and math courses (Zeidenberg et al., 2012). Finally, if more students taking and passing gateway courses equals more students graduating, then the ALP model or any of its variations should have resulted in higher graduation rates. This has not been demonstrated in any extant literature on corequisites (Cho et al., 2012; Ran & Lin, 2019).
Lowering the achievement objective to the new goal of passing gateway courses instead of the more widely accepted aim of graduating is only half of the bait and switch. The other half is that calculating “cost per successful student” in English composition has masked the true cost of the program. For example, Jenkins et al. (2010) estimated the “total cost per semester” to teach 250 traditional remedial students as $73,325, whereas they estimated it would cost $135,917 to teach 250 ALP students (p. 13). However, they went on to calculate each sum according to how many students pass the second college composition course. This quote shows how they transformed ALP’s actual costs into “less spending” and college “savings” (p. 14):
When compared to the traditional model in which students take developmental English and ENGL 101 sequentially, ALP provides a substantially more cost-effective route for students to pass the ENGL 101 and 102 sequence required for an associate degree ($2,680 versus $3,122). This difference of $442 per student represents 14% less spending by the college on a cohort of ENGL 052 students. Alternatively expressed, if the college enrolls 250 ENGL 052 students each year with the objective of getting them to pass ENGL 102, it will save $40,400 using the ALP method rather than the traditional model. (p. 14)
It is a slight stretch, first of all, to characterize “14% less spending” as “substantially more cost-effective” (Jenkins et al., 2010, p. 14). More critically, the calculation did not reflect the actual amount of money spent on the program. Regardless of “cost per successful student,” the total cost of ALP is still double the traditional model. The $135,917 number does not change depending on the denominator, nor would a college actually save $40,400 (p. 13). It would save no money.
In sum, ALP actually increases base spending by 100% or more. It is misleading for anyone to claim that the cost is cheaper under the ALP model. It is only cheaper when one sets the bar at passing a college-level gateway course instead of completion, and then calculates the cost per student passing a gateway course. Setting a lower bar and calculating costs unconventionally are types of bait and switch. Of course, an extremely persuasive argument could be made that higher education requires a great deal more funding to improve outcomes (Rosenberg, 2017), but to characterize a program that doubles the cost of remediation as saving money is disingenuous. This is especially true when one considers that there is no increase in graduation rates in return for doubling the cost (Ran & Lin, 2019).
Apples-to-Oranges Passrate comparisons: the Second Bait and Switch in Data Analysis
Almost every paper reporting on corequisites has claimed that the model has caused passrates in college-level courses to increase dramatically when compared to the traditional model. Some reports have claimed increases from 12 to 51% in math and 31 to 59% in English (Belfield et al., 2016). Others, such as CCA (Complete College America, n.d.), have stated that corequisites are doubling or tripling gatekeeper passrates. To take their most dramatic example, one CCA infographic shows a 22 to 71% increase in remedial English gateway passrates (Complete College America, n.d.). This is surprising for a relatively small intervention because increases such as these are quite rare in education. Even with thousands of institutions working very hard to increase college completion rates over the past eight years, those numbers have barely moved (Field, 2015). Annual college persistence rates in the nation are unchanged as well. It usually takes a large and well-funded intervention to move the needle in education.
Something other than the corequisite model itself might be contributing to these outsized increases. It turns out that half or more of these increases in college-level passrates may be due to researchers inadvertently engaging in yet another slight bait and switch in data analysis: the classic apples-to-oranges comparison. There are in fact several different apples-to-oranges comparisons going on in the various corequisite studies and data analyses that artificially exaggerate passrate increases.
In general comparisons, researchers first take a group of traditional prerequisite remedial students who enroll in and pass a stand-alone remedial English course initially, and then enroll in and pass the respective gatekeeper English course the following semester or later. Researchers then take a group of similar remedial students who volunteer to enroll in that same gatekeeper English course along with a companion course (the ALP model as described above), which, again, is not really traditional remediation, but instead is a course designed to help students pass the college-level course, with half the student-teacher ratio, more focus on noncognitives, and double the time on task. Researchers then compare the two groups’ passrates in the college-level English course. Figure 1 below is a hypothetical flowchart the CCRC includes in their most recent paper on the corequisite model in Tennessee (Belfield et al., 2016, p. 4):
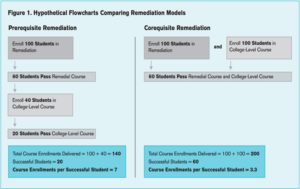
Put another way, researchers are comparing the passrates of a group of students who go through a set of two courses across two semesters (see left column), to a group of students who go through two courses in one semester (see right column). This is apples-to-oranges because of a very important factor called attrition. The number of students who do not come back in a successive semester at community colleges is high, and this alone could account for much of the increase in passrates when comparing a group of corequisite students to a group of traditional remedial students. In fact, in Figure 1, of the original group of 100 remedial students in the stand-alone course, 20 students do not even enroll in the college-level gateway course.
The chart below is a simpler way to conceptualize the apples-to-oranges comparison of traditional remediation and corequisite remediation. The left side shows a hypothetical progression of 100 prerequisite remedial students who start in a remedial course and then take and pass a gateway course. In this example, out of 70 who pass the traditional remedial course, only 50 take the corresponding gateway course. The right side shows that all 100 remedial students take both a companion course and a gateway course at the same time, and 70 pass both courses. The comparison, then, shows an increase in gateway passrates from 40 to 70. The fact that 20 students did not even attempt the gateway course is held against the remedial course. If the gateway passrate of the 40 students who originally took traditional remediation were compared with the ALP gateway passrate, it would be higher: 80% of traditional remedial students passed the gateway course versus only 70%.
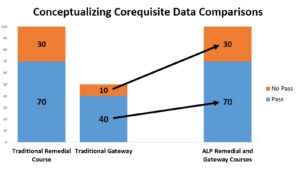
Part of the argument in defense of corequisites is that the model does not allow for students to drop out as much because there are “fewer exit points.” However, it is extremely important to understand that prerequisite remedial courses themselves are not causing these students to exit college. Many people are confusing causation with correlation and labeling remediation as a barrier, but it is well known that first-year college-level courses have equally low passrates and thus could be labeled as barriers as well (Yeado et al., 2014; Zeidenberg et al., 2012). It is also well understood that factors unrelated to courses at college are the main reasons students “stop out,” withdraw, or do not return the second semester (Johnson et al., 2011).
Therefore, when calculating the passrates of corequisites, it is a misrepresentation of data to include stopouts in the prerequisite remedial control group numbers. Researchers artificially inflate the passrates of the ALP model because the prerequisite group’s number includes stopouts that are not caused by prerequisite remediation. Withdrawals are a common result of attending multiple semesters of college, and proportionately, more withdrawals occur after the first semester of college than after subsequent semesters.
There are two other factors compounding the attrition comparison problem between the two groups in the ALP model (Cho et al., 2012). First, researchers compared a group of prerequisite remedial students who only received three hours of college composition per week to another group of similar remedial students who received six hours of college composition per week in the corequisite model. Second, the prerequisite group of remedial students had a student-teacher ratio of 20-1, and the corequisite group had a student teacher ratio of 8-1 in three of the six hours per week in the gateway course. The differences in time on task and student-teacher ratios between the two groups mean that there are too many variables affecting outcomes to make a sound comparison.
A different type of apples-to-oranges comparison problem can be found in the percentages on the CCA website “Spanning the Divide” (Complete College America, n.d.). As their infographics stated, CCA compared the national average of stand-alone remedial passrates to particular state corequisite passrates. It is impossible to correctly analyze an intervention if one does not compare two groups from the same pool of students, much less the same institution. Compounding the problem of comparing national averages to state averages was the inclusion of stopouts in the prerequisite remedial groups. Worse yet, none of the corequisite analyses in CCA data were randomized, controlled experiments, nor do they account for varying populations. Even the best constructed analyses of ALP have the methodological comparison problem of comparing a set of volunteer remedial students to a set of non-volunteer remedial students.
Apples-to-oranges comparisons can also be found with corequisite math model studies. For example, a recent study published in the journal Educational Evaluation and Policy Analysis (Logue et al., 2016) compared the outcomes of students from similar remedial backgrounds who were randomly placed into three math course designs: a traditional version of remedial elementary algebra (EA); a corequisite version of remedial elementary algebra which had a workshop added (EA-WS); and a corequisite version of college-level statistics which also had a workshop added (Stat-WS). The authors, Logue et al. (2016), took the elementary algebra workshop course passrate and compared it to the college-level statistics course passrate. Even though they accounted for the comparison problems of attrition and random assignment, they created a different apples-to-oranges problem because the two courses being compared teach completely different curricula.
In an Education Next overview of their study, Logue et al. (2017) cited higher passrates in the college-level statistics corequisite course and concluded that institutions and “policymakers should consider whether students need to pass remedial classes in order to progress to credit-bearing courses” (para. 28). Remarkably, the authors recognized the apples-to-oranges comparison when they stated, “Remedial elementary algebra and introductory statistics are qualitatively different classes, so it is not possible to compare their grading or difficulty directly” (para. 26). However, they persisted in arguing that the higher passrates of the corequisite college-level statistics course make it a better model. However, at least this study was conducted in a randomized controlled trial (RCT), the gold standard in research. It is rare to find RCTs in higher education.
Despite the group differences comparison problems, this study (Logue et al., 2016) deserves a closer look because it revealed two interesting results regarding corequisites. First, the researchers conducted a variation of corequisites that not typically associated with this course design. That is, they compared a group of students who took remedial elementary algebra (EA) to a group of like students who took EA with a mandatory weekly 2-hour workshop led by a trained workshop leader (EA-WS). The latter version was dubbed a corequisite because they define it as simply “additional academic support” (p. 580). As can be seen in Figure 2 (p. 588), the results of this workshop-based corequisite version showed that students passed the EA-WS course at a rate of 5.6 percentage points higher than EA students, which was a statistically insignificant increase. In other words, merely adding a workshop as a corequisite—even a two-hour lab led by trained assistants who join students in the regular class—may only modestly increase passrates, if at all.
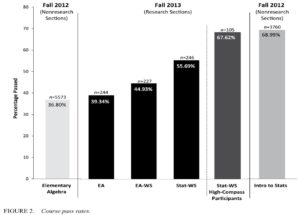
The second finding (Logue et al., 2016) was that only the students near the cutoff for the placement test (High-Compass Participants) passed the college-level statistics course at a rate similar to college-level students. The entire cohort of remedial students (Stat-WS) who took college-level statistics with a workshop “passed at a lower rate (55.69%) than did students who took introductory statistics at the three colleges in fall 2012 (68.99%)” (p. 587). Therefore, according to this research, a workshop model of corequisites for lower-level remedial students did not allow remedial students to perform as well as nonremedial students. At best, if only the highest-performing remedial students are chosen and provided a high-quality structured workshop, they may perform similarly to college-level students and better than lower-scoring remedial students, if this result is generalized.
However, this study is difficult to generalize and apply to other institutions because one does not know whether the results were due to instructor effects, the institutions’ math culture, or any other variable affecting the math passrates of the 12 instructors at the three different colleges who participated in the study (Logue et al., 2016). As an example of one of the most important but least-known factors that could impact passrates, I would like to relate an anecdote. I spoke with an instructor who used to be a graduate assistant teaching undergraduate math courses at a university. He told me the chair of the division told all graduate assistants that they were passing too many undergraduates. The next semester, more undergrads failed their math courses. I have also heard of similar bell-curve-type grading enforced in science divisions. Many institutions have explicit or implicit grading procedures that affect student passrates directly, yet may not have anything to do with course design, student ability, or student performance. Perhaps the way statistics is taught in CUNY as a culture lends itself to higher grades. Logue et al. (2016) controlled for these factors somewhat, but not completely.
Related to this, another apples-to-oranges comparison problem in math corequisites can be found in the preliminary results from Tennessee. As noted, Belfield et al. (2016) found that the corequisite math design in Tennessee caused remedial student passrates in college-level math to increase from 12% to 51% (p. 4). However, what is not highlighted is that at the same time the state implemented corequisites, they also switched the course most remedial students take from algebra to statistics:
Only 21 percent of the college-level courses taken by corequisite students were in algebra courses; most corequisite students enrolled in Probability and Statistics or Math for Liberal Arts. According to college officials, in the past, most incoming students were referred to an algebra path rather than these others. (p. 8)
What this means is that researchers (Belfield et al., 2016) compared the remedial passrate of 12% in algebra to the remedial passrate of 51% in statistics or liberal arts math corequisites. This comparison problem is very similar to Logue et al. (2016) study, in which they argue that remedial students pass college-level statistics at a higher rate than elementary algebra. More recent and in-depth research into the corequisite experiment in Tennessee (Ran & Lin, 2019) has demonstrated that, in fact, the increase in passrates in math can almost solely be attributed to the switch to statistics and not the corequisite model: “These findings suggest that the pathways effects are the dominating factor driving the overall positive effects of corequisite placement on math gateway course completion” (p. 27).
After reviewing the comparison and intervention groups in corequisite studies more closely, one could conclude that there is a fundamental problem: The corequisite model is almost incomparable to the traditional remediation model because they involve two entirely different courses and tracks that remedial students take. Another problem is that stopouts are included in the traditional track comparison and they are not included in the corequisite group’s numbers. Moreover, researchers are comparing a two-semester model to a one-semester model. Attrition is being counted in the traditional remedial model and not in the corequisite model.
Perhaps a better analysis would be to construct a comparison group in which traditional remedial students are allowed to volunteer to take a remedial course that has a student-teacher ratio of 8-1 and that has double the number of hours per week dedicated to outcomes. All of the other essential and beneficial aspects of the ALP model could be applied to this stand-alone prerequisite remedial course as well, such as the use of mostly full-time, highly trained instructors utilizing a common course sourcebook. Or, perhaps traditional remedial students could take an ALP-style gateway course with double the time on task and half the student-teacher ratio. It would be interesting to see how well these traditional remedial students performed in subsequent college-level courses after they receive similar interventions.
ALP Causes Increased college-level Failrates: A final unacknowledged Negative Outcome
There is one final factor hidden in the research of ALP that not many practitioners, administrators, and researchers discuss. It has to do with the model’s simultaneous increase in college-level passrates and college-level failrates. Indeed, even though college-level passrate numbers increased for remedial students under the overall corequisite model, sometimes by double or triple, the college-level failrates for those same remedial students also doubled, tripled, or more, depending on how low prerequisite passrates were to begin with.
Under the original ALP model, while students who placed into the corequisite model had nearly double the passrates in college-level English, they also had nearly double the failrates. The Cho et al. (2012) paper showed the raw numbers in Table 2 (p. 7):
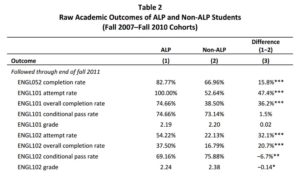
In this table of raw numbers, the ALP “ENGL101 [college-level gateway English] overall completion rate” was 74.66% (Cho et al., 2012, p 7). The overall completion rate for non-ALP students in that same course was 38.5%. However, only 52.64% of the non-ALP remedial students even enrolled in the college composition course. That means out of 100 original students under prerequisite remediation at CCBC, about 53 students took the college-level English course. Then out of those 53 students, about 39 passed the course. That means 14 students failed college-level English under CCBC’s traditional model.
Under the ALP model (Cho et al., 2012), all 100 remedial students took college-level English, and about 75 passed. That means 25 students failed the college-level English course. In exchange for an increase of college-level passrates from 39 to 75% (a 90% increase, which is nearly double), ALP caused remedial students’ failrates to increase from 14 to 25% (an 80% increase, which is also nearly double). The ALP model doubles remedial passrates and doubles remedial failrates in college-level English.
Add to this the failrates in the second college composition course (labeled ENGL102 in Table 2), and the overall failrate gets worse for ALP students (Cho et al., 2012). About 17 of a group of 100 ALP students failed ENGL102, whereas only 5 non-ALP students did. If these numbers are added to the first college-level English course results, that means 19% of non-ALP and 42% of ALP students failed in ENGL101 or ENGL102. The ALP model caused well over double the number of students to fail a college-level English course.
If this same type of calculation is applied to the Belfield et al. (2016) flowchart (see Figure 1 above), the failrates in college-level courses are even higher. Under the prerequisite remediation model, only 10 students out of a 100 failed the college-level course because only 20 took it and only 10 passed it. Under the corequisite model, all 100 took the college-level course and only 60 passed. That means 40 failed the college-level course. In return for a passrate that increased from 10 to 60%, the fail rate increased from 10 to 40%. Tennessee corequisites might have increased passrates a great deal, but quadrupling failrates in college-level courses was not a positive outcome. Add to this the potential increase in failrates in any second-semester courses, as outlined in the ALP model, and the failrates in the first year alone could be six times higher, equaling the passrate increase.
These difficult questions must now be addressed: Are policymakers satisfied with doubling or tripling the number of college-level passes for some remedial students, when also doubling or tripling college-level failrates for other students? What is the effect of college-level fails on those students? Overall, is it worse than the low gateway passrates of traditional remediation? In other words, there may be additional consequences for those students who have fails in college-level credits as a result of being put into gateway courses while underprepared. Their GPAs may begin lower, their grades may stay lower than they might have otherwise, their confidence may be lower (a charge leveled at remedial courses continually), and it may negatively affect their financial aid (another charge leveled at remediation). No research to date has been conducted on the consequences of failrate increases resulting from the corequisite model.
a misapplication of the ALP research: The Real Bait and Switch
The wide-spread sharing of the ostensible success of ALP has led many states to hastily implement variations of the original ALP corequisite model, most of which do not include the more beneficial components of the program. These variations are probably being implemented because states and institutions cannot afford to invest double the money on instruction, nor do they have the time and resources to coordinate and monitor the extensively prepared and researched ALP model (Adams et al., 2009; Cho et al., 2012; Jenkins et al., 2010). However, it is very likely that some organizations and institutions are using the corequisite reform movement as a means by which to eliminate or severely restrict remediation and instead put as many students into college-level courses as possible.
Either way, what results is a misapplication of good research. Institutions and organizations such as CCA will cite CCRC data on ALP, claim that the corequisite model is a research-based reform, and then proceed to implement different models of corequisites, most of which have no basis in existing reputable data. This is the education equivalent of an actual bait and switch.
A perfect example of this can be found in a recent document on corequisites released by the Oklahoma State System of Higher Education (2016). In this overview, the State of Oklahoma recommended four versions of corequisites that the state’s institutions of higher education have adopted and implemented by Fall 2017. Below are the four options (p. 2):

Each of the three variations is significantly different from the ALP model initially studied, and even the recommended ALP model is different. Since institutions might employ one or more of these recommendations, they need to be explored more thoroughly.
Variation 1
In the first bullet, the wording of the ALP model stated that the “same instructor usually teaches both courses,” which implies that it is acceptable to implement a model which does not have the same instructor teaching both courses. This is a switch in the model that may cause declines in passrates because it has not been studied. The State of Indiana has also mandated corequisite remediation in their system of higher education, and they, too, do not require both courses to be taught by the same instructor.
Variation 2
In the second bullet, the mandatory tutoring or lab option essentially recommends that institutions move remedial students into college-level courses and add a one-hour or two-hour tutoring or lab session per week. It does not state which levels of remedial students should be placed into this model, so conceivably, even the lowest-level remedial student might be placed into a college-level course with a one-hour noncredit lab hour. What will be covered in this lab hour is not known, but one can assume that students will complete homework and request assistance when needed. There is some research suggesting that tutor centers can help, but this variation has the potential to harm many at-risk students. Tutoring or self-paced lab work for an hour or so per week can only help remedial students in college-level courses so much. For those whose goal it is to eliminate remediation, this option is reminiscent of the right to fail.
This lab corequisite variation will probably be the most popular choice of reform due to the ease of its implementation and its low cost. Institutions could simply require all new students who place into remedial courses to take college-level courses along with a mandatory lab hour. The only investment they would have to make is to add lab assistants in their tutor centers and monitor attendance. It has the potential to affect a large number of at-risk students almost immediately.
Therefore, to explore the second bullet further, Logue et al. (2016) is helpful. In that study, there were two versions of corequisites, one of which added a two-hour workshop to a remedial math course, and one which added a two-hour workshop to a college-level course designed for remedial students. These workshops were led by trained assistants who sat in with students in the regular courses and who interacted with instructors on a weekly basis. The Oklahoma version of “mandatory tutoring” did not recommend this highly structured approach to tutoring (Oklahoma State System, 2016). It merely recommended a one- or two-hour lab or tutoring session. However, one can estimate the effects of structured workshops on math students using Figure 2 from their study (p. 588) (arrows and analysis added):

Remedial students who took elementary algebra (EA) without a workshop passed at a rate of 39%, whereas similar remedial students who took the same course with a two-hour workshop (EA-WS) passed at a rate of 45% (Logue et al., 2016). This increase is modest yet statistically insignificant. In the statistics course corequisite model, remedial students who took college-level statistics with a workshop (Stat-WS) passed at a rate of 56%, whereas nonremedial students who took statistics without the workshop passed at a rate of 69%. In other words, remedial students who took a college course with a workshop passed at a statistically significantly lower rate than the college-level students who took the same course without a workshop. The workshop in the college course did not help remedial students perform as well as nonremedial students. The authors note, however, that the students who took Stat-WS were remedial students equal in almost every way to the ones who took EA and EA-WS, yet they passed a college-level course at a higher rate than the EA-WS. Finally, looking only at the highest remedial students from the Stat-WS group (High-Compass Participants), one will find that they passed their college-level stats course at a rate equal to the nonremedial students.
There are two important takeaways from this study. The first takeaway is that highly structured workshops for remedial students in college-level courses may work well only with those who are just beneath a college-level cutoff. Structured workshops may only slightly improve college-level outcomes for students further down the remedial placement test range, but they will not allow lower-level remedial students to perform as well as college-level students. If those structured workshops are replaced with an unstructured, self-paced lab hour, then outcomes will likely be lower. A model like this could in fact increase college-level course failrates significantly without improving outcomes at all. The second takeaway is that if a two-hour highly structured workshop is utilized in a traditional remedial math course, those students will see a modest but statistically insignificant gain in passrates.
Variation 3
The third bullet is a variation of simple acceleration, yet this type of acceleration is not common, nor has it been tested. As opposed to typical remedial acceleration, which may take two remedial semester-long courses and compress them into one semester, this version compresses both the remedial course and the college-level course into one semester. It may be quite harmful for remedial students to take a compressed college-level course immediately after a compressed remedial course because it would reduce the time on task in the college-level course, the exact opposite of one of ALP’s key features (Cho et al., 2012). The typical model of acceleration has been studied by the CCRC and has been deemed to have “moderate evidence” by the What Works Clearinghouse (Bailey et al., 2016). However, this variation is taking a remedial course and compressing it into five weeks, with the remainder of the semester dedicated to a compressed college-level course, and it has no evidence to support it.
Variation 4
Remarkably, bullet four is essentially the traditional remediation model. The difference here is that the remedial course and the college-level course would align their outcomes and objectives more closely. One would expect that institutions would have been doing this all along as a best practice, regardless of this recommendation, but it is well known that many remedial courses are not aligned properly with college-level courses. The surprising part about this variation is that is included in both the acceleration and corequisites categories. Clearly it is neither.
Any researcher will state that one cannot expect similar results from a study when one does not replicate that study in almost every detail. Therefore, it is unclear how the State of Oklahoma or Indiana, or any of the numerous other states involved in corequisite reform (Georgia, Tennessee, Texas, California, etc.), can expect their corequisite variations to have similar outcomes as the ALP model, especially when subsequent results such as persistence, credit accumulation, and completion are considered. These variations may simply temporarily increase passrates, simultaneously increase failrates, cost a great deal more, and have no effect on graduation. It may even negatively affect graduation rates, considering that ALP had a small negative effect on certificate completion for remedial students and on transfer rates for nonremedial students (Cho et al., 2012).
It must be noted that the particular initiative in Oklahoma (Oklahoma State System, 2016) was created and fostered by Complete College America (CCA), which has funding by the Lumina Foundation, the Michael and Susan Dell Foundation, the Bill and Melinda Gates Foundation, the Kresge Foundation, and the Carnegie Corporation of New York. Furthermore, what is happening in Oklahoma right now has already happened in many states, such as Georgia, West Virginia, Tennessee, Indiana, California, Texas, and Colorado. Again, CCA has also released “data” showing an increase in remedial passrates in college-level courses as a result of the implementation of various models across the nation. Unfortunately, these numbers suffer from many flaws. One can view the basis for these variations in a document entitled “Core Principles for Transforming Remediation within a Comprehensive Student Success Strategy” (ECS, 2015), but it is quite clear that CCA’s rhetoric is decidedly biased against remediation (“Remediation,” 2012). Knowing full well that institutions will typically choose the easiest and most inexpensive option from any available reforms, CCA is most likely using ALP as a basis to simply restrict or eliminate remediation.
Surprisingly, as further support for those who wish to eliminate remediation, even the CCBC’s current ALP model has decided to eliminate prerequisite remediation (ALP, n.d.-a). It can be assumed that this current ALP model still employs all the supports from the original. However, if other institutions cite the current ALP model and put even the lowest-level remedial student into college-level courses, but instead require one hour of lab time as opposed to all the beneficial components, the result will probably be harmful for these lower-level at-risk students.
A Top Government Research Organization excluded CCRC Research on ALP
Perhaps the most surprising and little-known fact about the research on ALP is that the What Works Clearinghouse (WWC), the research and statistics division of the Institute for Education Sciences (IES), did not classify the research on ALP as meeting their standards for rigorous research. As can be read in the WWC Procedures and Standards Handbook,
The WWC is an important part of IES’s strategy to use rigorous and relevant research, evaluation, and statistics to improve our nation’s education system. It provides critical assessments of scientific evidence on the effectiveness of education programs, policies, and practices (referred to as “interventions”) and a range of products summarizing this evidence. (p. 1)
Thomas Bailey, the former director of several Columbia University’s Teachers College research organizations, CCRC, NCPR, CAPR, and CAPSEE (the latter two of which are the IES-funded research organizations with grants awarded after the CCRC and NCPR became more popular), in conjunction with several other researchers, recently published a What Works Clearinghouse paper on developmental education recommendations. It is called “Strategies for Postsecondary Students in Developmental Education – A Practice Guide for College and University Administrators, Advisors, and Faculty” (Bailey et al., 2016).
In this document, Bailey et al. (2016) outlined six recommendations to improve remedial outcomes in higher education. Recommendation 4 was to “compress or mainstream developmental education with course redesign,” and a major part of this recommendation is the corequisite model, including ALP and its variations. In spite of its inclusion in this document, the researchers at the WWC only rated this recommendation as having “minimal evidence” to support its use: “Summary of evidence: Minimal Evidence: The panel assigned a rating of minimal evidence to this recommendation” (p. 36). In fact, three of the six total recommendations from the entire document were assigned a minimal evidence rating, and the other three were assigned a “moderate evidence” rating. None had the highest WWC rating for research, which is “strong.”
Upon further investigation of the research behind acceleration in Recommendation 4, as can be found in Appendix D, Appendix Table 4, Bailey et al. (2016) cited only five studies. However, as can be read in the footnotes, four of the five studies cited in support of acceleration “did not meet WWC standards” (pp. 90–92). The only one that did meet WWC standards was an article on a shortened sequence of remedial courses in New York, yet this paper still only met “WWC Group Design Standards With Reservations” (p. 90). Thus, the sole study that allowed corequisites to gain even a minimal rating had nothing to do with corequisites.
It is difficult to understand why the authors, in a paper published by the USDOE, the Institute for Education Sciences, the National Center for Education Statistics, and the What Works Clearinghouse, would endorse a corequisite model recommendation in a paper with no WWC-approved evidence to support it. In fact, both CCRC ALP papers from 2010 and 2012 (Cho et al., 2012; Jenkins et al., 2010) were included in the five studies Bailey et al. (2016) cited, yet neither met WWC standards.
Weighing All the pros and cons
The corequisite model in its entirety is indeed quite complicated. There are a great deal of moving parts, and each part requires an in-depth explanation to understand its effect on the whole. To sum up, however, this is a comprehensive list of pros and cons:
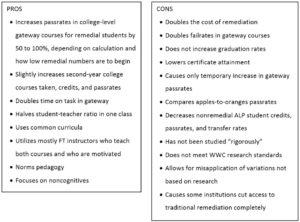
The primary and most-repeated benefit of ALP or its variations in the corequisite reform movement is that it increases passrates in gatekeeper courses. However, any positive result of a reform must be carefully weighed with its accompanying negatives before one considers implementing the entire reform, or even a part of it. It is too easy to overlook the negatives when focusing on the positive aspects alone.
Imagine if someone were to approach an administrator or legislator and say the following:
I have a reform that will increase passrates for remedial students in gateway English courses anywhere from 50 to 100%, depending on how it is calculated and where our passrates are currently. It involves doubling the time on task in the gateway course and halving the student-teacher ratio for upper-level remedial students. In addition to doing better than traditional remedial students in the gateway course, these students might even perform better in their second semester. On the other hand, it will cost the college and taxpayers double, it will double failrates in those gateway courses for other remedial students, its effects will be temporary, it will not lead to increased graduation rates, it will slightly harm the nonremedial students, and even the researchers who conducted studies on this reform claim that their research is not rigorous. In fact, the studies conducted on it do not even meet the government’s What Works Clearinghouse standards for research.
When ALP is described this way, it is difficult to believe that anyone would argue the corequisite movement is the miraculous reform its advocates are claiming it is. One could almost guarantee that an administrator or legislator would reject it. The phrases “cost the college and taxpayers double,” “double failrates,” and “not lead to increased graduation rates” are deal-breakers for most decision-makers.
Worse yet, imagine if that same person were to continue describing the variations of the reform:
In spite of the lack of rigorous research into the ALP reform specifically, and despite the fact that many negative outcomes accompany the few positive results, institutions and entire states are moving forward with the implementation of several variations of this reform, almost none of which have any basis in research. What are your thoughts about going along with this?
A researcher would respond that it might be a better idea to scale up a workable, cost-effective variation in one or several locations first, and then implement it at a larger scale, much like the CUNY ASAP model, which was successfully replicated in Ohio (Miller et al., 2020) and is being scaled elsewhere. The studies that have been conducted with ASAP have met WWC standards with no reservations and were randomized controlled trials, the gold standard in research. Any corequisite variations, before they are implemented hastily in the nation, should undergo such rigorous study with larger numbers of students.
If Corequisites are Going to be implemented, What parts of the model are most important?
If institutions are going to implement this model before further research is conducted, it is important that almost all the aspects of the original program remain intact because no one can be sure which factors contribute most to the increased rates of gatekeeper success. It may be safe to assume that there are several key components of the ALP model that lead to an increase in English gateway course passrates. Thus, if these crucial parts to the program are included in a variation of the reform, perhaps the results will be similar to ALP’s.
First and most important is the fact that students who enroll in the ALP model of English are actually taking six credits of college composition. This doubles the time on task in gatekeeper English. A good argument could be made that this practice should be adopted in many more gatekeeper courses because many first-year, first-semester courses at any college suffer from low passrates (Zeidenberg et al., 2012). Any corequisite model should double the time on task in the gateway course for remedial students.
Second, the student-teacher ratio in the ALP model studied was 8-1 (Jenkins et al., 2010). ALP’s current model has a 10-1 student-teacher ratio (ALP, n.d.-b), and one could assume that this will not change the outcomes. Whether 8-1 or 10-1, a low student-teacher ratio is very important, and this component is perhaps the most disregarded part of the model when it is implemented in other institutions. Institutions choosing to start any corequisite variations would do well to utilize this crucial component.
Third, the same highly qualified instructor teaches both the college-level course and the companion course, and that instructor uses well-developed materials. This, too, is not being followed in many states. Instead, students are often taught by adjuncts who may not even know the instructor of the college-level course, let alone be familiar with the content or delivery of the college-level course itself. Moreover, the curricula of the two courses in an ALP model should be thoroughly developed, and the instructors of the course should be familiar with both curricula.
Finally, in all the reputable research on ALP and corequisite variations, the benefits of corequisites are best for remedial students just beneath the college-level cutoff (Cho et al., 2012; Ran & Lin, 2019). Lowering the bar for remedial students to take college-level courses, especially in conjunction with a self-paced lab hour alone, much like bullet two from Oklahoma (Oklahoma State System, 2016), may be a recipe for only increasing failrates in college-level courses and not helping student outcomes in college overall. Logue et al.’s (2016) research clearly demonstrated that a two-hour structured lab in a college statistics course will only be beneficial for remedial students just beneath the college-level cutoff. Again, their study is the only randomized controlled trial in education to date which isolated the effect of a corequisite lab on remedial students in both remedial math and college-level math courses. Therefore, it is the best resource policymakers can use to predict what will happen if institutions implement structured labs in courses.
A factor to avoid might be the “mainstreaming” (Adams et al., 2009) or “co-mingling,” as it has been termed, of remedial and nonremedial students in the same course. Clearly there are negative outcomes for the nonremedial students who are placed into college-level courses with remedial students in the ALP corequisite model (Cho et al., 2012). Perhaps an alternative would be to put only remedial students who place just beneath the college cutoff into a college-level course which doubles the time on task and has a lower student-teacher ratio. Since the ALP version has a 20-1 student-teacher ratio for three credits and an 8-1 for three credits, perhaps a model with a 15-1 ratio of all remedial students could be employed to maximize benefits and reduce costs.
There are several other components that contribute to ALP’s limited positive results, but these appear to be the most important. Again, unfortunately, most versions of corequisites in the nationwide movement do not include most of these core components. Institutions that have been persuaded to implement variations of corequisites may have been baited with promising results from research-based reforms, but then have been misled, intentionally or unintentionally, by switches to reforms that do not have data supporting them. In order to ensure the quality of instruction for at-risk students, institutions should avoid putting remedial students into college-level courses without the appropriate and well-supported network of support.
Applying what works from alp more broadly
If institutions are unable to implement the original ALP model, with all its beneficial components and its framework of support, then they still may be able to take away lessons that will help them improve any variations they may be considering in its place. Perhaps the best lesson policymakers and practitioners can take from corequisite studies is that doubling deliberate practice and time on task in a class will most likely help students achieve course objectives. Another lesson is that reducing student-teacher ratios can have a dramatic effect on students. Since eight to 10 remedial students take two courses with one instructor, this model also resembles a learning community (LC), a model which allows students to work together in two or more courses. The LC model has been shown to increase student engagement and their ability to acclimatize socially to college, as well as some other limited positive outcomes (Weiss et al., 2014). Finally, normed and thoughtful common curricula may help tremendously to improve quality and standards in gatekeeper courses.
An overall lesson one can take from the preliminary studies on corequisites, moreover, is that regardless of the type of class or level, these smaller components may work well in any higher education course design and pedagogy. In other words, policymakers and practitioners should be taking what works in remedial reforms and applying it to other first-year courses at community colleges and open admissions universities. However, when implementing variations of reforms that have been studied, institutions should never assume that a greatly truncated version will result in similar outcomes. The more one cuts from a holistic reform, the less one should expect in return. Also, if research is implemented improperly and cheaply, institutions may end up harming at-risk students instead of helping them.
Therefore, institutions should avoid being baited with well-implemented and data-based reforms, switching them into easy and low-cost changes, and believing that they will result in similar outcomes. In order to achieve more dramatic and lasting increases in outcomes, such as graduation and transfer rates, institutions may need to invest a great deal more in thoughtful remedial and college-level course design, in research and data analysis, and in students directly. This runs counter to the current movement of doing more with less in higher education, but thus far, the data suggest only comprehensive and well-funded reforms work best.
References
Accelerated Learning Program (ALP). (n.d.-a). Important change in the ALP model. http://alp-deved.org/2016/08/important-change-in-the-alp-model/
Accelerated Learning Program (ALP). (n.d.-b). What is ALP exactly? http://alp-deved.org/what-is-alp-exactly/
Adams, P., Gearhart, S., Miller, R., & Roberts, A. (2009). The Accelerated Learning Program: Throwing open the gates. Journal of Basic Writing, 28(2), 50–69. http://files.eric.ed.gov/fulltext/EJ877255.pdf
Aschwanden, C., & King, R. (2015, August 9). Science isn’t broken. Five Thirty Eight. http://fivethirtyeight.com/features/science-isnt-broken/
Bailey, T., Bashford, J., Boatman, A., Squires, J., Weiss, M., Doyle, W., Valentine, J. C., LaSota, R., Polanin, J. R., Spinney, E., Wilson, W., Yeide, M., & Young, S. H. (2016). Strategies for postsecondary students in developmental education – A practice guide for college and university administrators, advisors, and faculty. Institute of Education Sciences, What Works Clearinghouse. http://ies.ed.gov/ncee/wwc/Docs/PracticeGuide/wwc_dev_ed_112916.pdf
Belfield. C. R., Jenkins, D., & Lahr, H. (2016). Is corequisite remediation cost effective? Early findings from Tennessee (CCRC Research Brief No. 62). Community College Research Center, Teachers College, Columbia University. https://ccrc.tc.columbia.edu/media/k2/attachments/corequisite-remediation-cost-effective-tennessee.pdf
Chickering, A. W., & Gamson, Z. F. (1987). Seven principles for good practice in undergraduate education. American Association for Higher Education Bulletin, 3–7. http://files.eric.ed.gov/fulltext/ED282491.pdf
Cho, S.W., Kopko, E., Jenkins, & C., Jaggars, S. (2012). New evidence of success for community college remedial English students: Tracking the outcomes of students in the Accelerated Learning Program (ALP) (CCRC Working Paper No. 53). Community College Research Center, Teachers College, Columbia University. http://ccrc.tc.columbia.edu/media/k2/attachments/ccbc-alp-student-outcomes-follow-up.pdf
Complete College America. (n.d.). Spanning the divide. http://completecollege.org/spanningthedivide/
Complete College America. (2012). Remediation: Higher education’s bridge to nowhere. Bill & Melinda Gates Foundation. https://eric.ed.gov/?id=ED536825
Duckworth, A. L., & Yeager, D. S. (2015). Measurement matters: Assessing personal qualities other than cognitive ability for educational purposes. Educational Researcher, 44(4), 237–251. http://journals.sagepub.com/doi/pdf/10.3102/0013189X15584327
Education Commission of the States. (2015, November 10). Core principles for transforming remediation within a comprehensive student success strategy: A joint statement. https://www.insidehighered.com/sites/default/server_files/files/core_principles_nov5.pdf
Fain, P. (2012, April 4). How to end remediation. Inside Higher Ed. https://www.insidehighered.com/news/2012/04/04/connecticut-legislature-mulls-elimination-remedial-courses
Field, K. (2015, January 20). 6 years in and 6 to go, only modest progress on Obama’s college-completion goal. The Chronicle of Higher Education. https://www.chronicle.com/article/6-Years-in6-to-Go-Only/151303
Goodlad, J. I. (1984). A place called school: Prospects for the future. McGraw-Hill.
Goudas, A. M. (2019). The corequisite model: Origins, evolution, data, and net effects. National Organization for Student Success Practitioner to Practitioner, 10(1), 3–10. https://thenoss.org/resources/Documents/NOSS%20Practitioner/NOSS%20Practitioner%20to%20Practitioner%20Winter%202019%20first.pdf
Ioannidis, J. P. A. (2005). Why most published research findings are false. PLoS Med, 2(8): e124. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1182327/
Jenkins, D., & Bailey, T. (2017). Early momentum metrics: Why they matter for college improvement (CCRC Brief No. 65). Community College Research Center, Teachers College, Columbia University. https://ccrc.tc.columbia.edu/media/k2/attachments/early-momentum-metrics-college-improvement.pdf
Jenkins, D., Speroni, C., Belfield, C., Jaggars, S., & Edgecombe, N. (2010). A model for accelerating academic success of community college remedial English students: Is the accelerated learning program (ALP) effective and affordable? (CCRC Working Paper No. 21). Community College Research Center, Teachers College, Columbia University. https://files.eric.ed.gov/fulltext/ED512398.pdf
. Educational Evaluation and Policy Analysis, 38(3), 578–598. http://journals.sagepub.com/doi/pdf/10.3102/0162373716649056
Miller, C., Headlam, C., Manno, M., & Cullinan, D. (2020). Increasing community college graduation rates with a proven model: Three-year results from the Accelerated Study in Associate Programs (ASAP) Ohio demonstration. MDRC. https://www.mdrc.org/sites/default/files/ASAP_OH_3yr_Impact_Report_1.pdf
Nosek, B. (2015). Estimating the reproducibility of psychological science. Science, 349(6251). http://science.sciencemag.org/content/349/6251/aac4716
Oklahoma State System of Higher Education. (2016). Corequisite at scale guidance.
Procedures and standards handbook version 3.0. What Works Clearinghouse. Washington, D.C.: U.S. Department of Education. Institute of Education Sciences, National Center for Education Statistics. Retrieved from https://ies.ed.gov/ncee/wwc/Docs/referenceresources/wwc_procedures_v3_0_standards_handbook.pdf
Ran, F. X., & Lin, Y. (2019). The effects of corequisite remediation: Evidence from a statewide reform in Tennessee (CCRC Working Paper No. 115). Community College Research Center, Teachers College, Columbia University. https://ccrc.tc.columbia.edu/media/k2/attachments/effects-corequisite-remediation-tennessee.pdf
Rosenberg, T. (2017, March 17). When a few bucks can get students to the finish line. The New York Times. https://www.nytimes.com/2017/03/14/opinion/when-a-few-bucks-can-get-students-to-the-finish-line.html
Russell, A. (2011). A guide to major U.S. college completion initiatives. American Association of State Colleges and Universities: A Higher Education Policy Brief. https://www.isac.org/e-library/research-policy-analysis/Task-Forces-Working-Groups/map-advising-workgroup/documents/Guide%20to%20college%20completion%20initiatives.pdf
Scrivener, S., Weiss, M. J., Ratledge, A., Rudd, T., Sommo, C., & Fresques, H. (2015). Doubling graduation rates: Three-year effects of CUNY’s Accelerated Study in Associate Programs (ASAP) for developmental education students. MDRC. http://www.mdrc.org/sites/default/files/doubling_graduation_rates_fr.pdf
Shafer, T. (2011). Developing expertise through a deliberate practice project. International Journal of Interpreter Education, 3, 17–27. http://www.interpretereducation.org/wp-content/uploads/2016/01/Deliberate-Practice-Article.pdf
Vandal, B. (2015, June 23). The results are in. Corequisite remediation works. Complete College America. https://completecollege.org/article/the-results-are-in-corequisite-remediation-works/
Weiss, M. J., Mayer, A., Cullinan, D., Ratledge, A., Sommo, C., & Diamond, J. (2014). A random assignment evaluation of learning communities at Kingsborough Community College: Seven years later. MDRC. http://www.mdrc.org/sites/default/files/A_Random_Assignment_Evaluation_of_Learning_Communities_KCC.pdf
Yeado, J., Haycock, K., Johnstone, R., & Chaplot, P. (2014). Higher education practice guide: Learning from high-performing and fast-gaining institutions. The Education Trust. http://edtrust.org/wp-content/uploads/2013/10/PracticeGuide1.pdf
Zeidenberg, M., Jenkins, D., & Scott, M. A. (2012). Not just math and English: Courses that pose obstacles to community college completion (CCRC Working Paper No. 52). Community College Research Center, Teachers College, Columbia University. http://ccrc.tc.columbia.edu/media/k2/attachments/not-just-math-and-english.pdf